Eine Kundin möchte bei Ihnen als Kreditsachbearbeiter einen Kredit über 15.800,00
EUR aufnehmen. Dabei gelten folgende Konditionen:
- Zinsen: 0,54 % p.m.
- Bearbeitungsgebühr: 2%
Die Kundin wünscht eine Laufzeit von 40 Monaten. Unterbreiten Sie einen Tilgungsvorschlag.
Die monatlichen Raten sollen über glatte 10 EUR lauten. Die erste
Ausgleichsrate soll geringer als die Folgeraten sein.
|
Lösung zu 1:
| Höhe Ratenkredit: |
|
15.800,00 EUR |
Bearbeitungsgebühr
(2% auf den Kreditbetrag): |
+ |
316,00 EUR |
Zinsaufwendungen
(0,54% x 40 Monate): |
+ |
3.412,80 EUR |
| Gesamtkosten Ratenkredit |
= |
19.528,80 EUR |
|
Die Gesamtkosten des Ratenkredits belaufen sich auf 19.528,80 EUR.
Um die monatliche Ratenhöhe auszurechnen, werden die Gesamtkosten
von 19.528,80 EUR durch die Laufzeit von 40 Monate geteilt.
Das Ergebnis ist die monatliche Rate = 488,22 EUR.
Die monatliche Belastung soll allerdings auf glatte 10 EUR lauten.
Die Lösung heißt also 39 Raten à 490,00 und 1 Rate à 418,80 EUR.
|
|
Aufgabe 2:
Die Kundin aus Fall Nr. 1 möchte höchstens 350,00 EURO im Monat als Rate leisten.
Wie lang müßte dann die Laufzeit gewährt werden und
wie sieht dann der Tilgungsplan aus ?
|
Lösung zu Aufgabe 2:
Die Lösung zu Aufgabe 2 kann nach folgender Formel erfolgen:
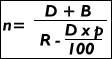
n = Anzahl der Raten
D = Darlehensbetrag
B = Bearbeitungsgebühr
|
R = Höchstrate
p = Zinssatz pro Monat
|
|
Danach ergibt sich folgende Rechnung:
n = 15.800,00 + 316,00 / [350 - (15.800,00 x 0,54 / 100)]
Das Ergebnis lautet 60,89 = 61 Raten.
Der Tilgungsplan kann wie folgt aussehen: 60 Raten à 350,00 und 1 Rate à 320,52.
|
|
Aufgabe 3:
Herr Mustermann hat vor einem Jahr einen Ratenkredit in Höhe von 5.000,00 EUR aufgenommen.
Die Gesamtschuld beträgt unter Berücksichtigung der Zinsen
bei 36 Monaten Laufzeit und einmaliger Bearbeitungsgebühr von 2
% 5.820,00 EUR. Wie hoch ist der zugrundeliegende Zinssatz ?
|
Lösung zu Aufgabe 3:
Die Differenz zwischen Kreditbetrag und tatsächlicher Kredithöhe
beträgt
820,00 EUR (5.820,00 - 5.000,00 EUR)
.
Folgerichtig sind die 820,00 EUR Zinsen und Bearbeitungsgebühr.
Von der Bearbeitungsgebühr wissen wir, dass sie 2 % von 5.000,00 EUR beträgt = 100,00 EUR.
820,00 EUR - 100,00 EUR = 720,00 EUR Zinsen
Zinsrechnungsformel:
p (Zinssatz) = Z (Zinsen) x 100 / K (Kapital)
Demnach ergibt sich folgende Rechnung:
p = 720,00 EUR x 100 / 5.000,00
Als Ergebnis erhält man 14,4 %. Dies sind die Zinsen für die Gesamtlaufzeit von 36 Monaten.
Um den Zinssatz p.m. zu errechnen, werden die 14,4 % / 36 Monate = 0,4 % p.m.
|
|
Aufgaben zur Ratenkreditberechnung:
Aufgabe 1:
Ein Kunde nimmt einen Ratenkredit zu folgenden Konditionen in Anspruch:
- Zinssatz: 0,5 % p.m.
- Bearbeitungsgebühr: 2 %
- Rückzahlung in 36 Monatsraten
- Ratenhöhe: 700,00 EUR
Wieviel EUR erhielt der Kunde ausgezahlt ?
Aufgabe 2:
Ein Kunde nimmt einen Ratenkredit in Höhe von 15.000,00 EUR auf, den er in 47 Monatsraten
zu je 383,00 EUR und einer Restrate zu 389,00 EUR zurückzahlt. Die Bearbeitungsgebühr
beträgt 1 %.
Mit wieviel Prozent p.m. wird der Kredit verzinst ?
| a) 0,44 % |
d) 0,50 % |
| b) 0,45 % |
e) 0,60 % |
| c) 0,42 % |
f ) 0,47 % |
|
Aufgabe 3:
Ein Kreditinstitut gewährt einen Ratenkredit über 4.400,00 EUR mit einer Laufzeit
von 32 Monaten, Zinsen 0,5 % p.m. vom ursprünglichen Darlehensbetrag, 2 % Bearbeitungsgebühr.
a) Unterbreite dem Kunden einen Tilgungsvorschlag. Die Raten sollen auf glatte
EURO abgerundet werden.
b) Berechne die Effektivverzinzung in Prozent p.a. (ohne Bearbeitungsgebühr).

c) Berechne die Effektivverzinzung in Prozent p.a. (mit Bearbeitungsgebühr).

Aufgabe 4:
Ein Kreditinstitut gewährt einen Ratenkredit über 7.200,00 EUR mit einer Laufzeit
von 30 Monaten, Zinsen 0,32 % p.m. vom ursprünglichen Darlehensbetrag, 2 % Bearbeitungsgebühr.
a) Unterbreite einen Tilgungsvorschlag. Die Raten sollen auf glatte EURO aufgerundet
werden.
b) Berechne die Effektivverzinzung in Prozent p.a. (ohne Bearbeitungsgebühr).
c) Berechne die Effektivverzinzung in Prozent p.a. (mit Bearbeitungsgebühr).
Aufgabe 5:
Ein Kunde nimmt einen Ratenkredit in Höhe von 3.800,00 EUR in Anspruch. Die Gesamtschuld
beträgt unter Berücksichtigung der Zinsen für 30 Monate
und der Bearbeitungsgebühr von 2 % 4.240,80 EUR.
Wie hoch ist der monatliche Zinssatz ?
Die Lösungen zu den Aufgaben:
Aufgabe 1:
Der Kredit wird in 36 Monatsraten à 700,00 EUR zurückgezahlt.
Insgesamt beträgt die Kredithöhe also 36 x 700 = 25.200 EUR.
Der Zinssatz für die Gesamtlaufzeit beträgt 18,00 % (0,5 % x 36 Monate). Die Bearbeitungsgebühr schlägt mit 2 % zu Buche.
Der zugrundeliegende Kreditbetrag entspricht 100 %. Zu diesen 100 % kommen aber noch die
Zinsen (18 %) und die Bearbeitungsgebühr (2 %) hinzu, so dass die
Gesamtschuld 120 % entspricht.
Dreisatz: 25.200,00 x 100 / 120 = 21.000,00 EUR
Der Kunde erhielt 21.000,00 EUR (=100 %) ausgezahlt.
Aufgabe 2:
Die gewünschte Ratenkredithöhe beträgt 15.000,00 EUR.
Der Ratenkredit wird in 47 Monatsraten à 383,00 EUR und 1er Restrate
von 389,00 EUR zurückgezahlt, was eine Gesamthöhe des Ratenkredits
von 18.390,00 EUR (383,00 x 47 + 389,00) ergibt.
Der Kunde muss also 3.390,00 EUR Zinsen und Bearbeitungsgebühr (18.390,00 - 15.000,00) zahlen.
Die Höhe der Bearbeitungsgebühr ist uns ebenfalls bekannt:
1 % vom ursprünglichen Kreditbetrag = 150,00 EUR.
Es bleibt also ein Restbetrag von 3.240,00 EUR = Zinsen.
Zinssatz = 3.240,00 x 100 / 15.000,00
Dies ergibt einen Gesamtzinssatz von 21,6 %. Monatlich bedeutet dies einen
Zinssatz von 0,45 %.
Damit ist Antwort (b) richtig.
Aufgabe 3:
a)
| Kreditbetrag: |
= |
4.400,00 EUR |
| Bearbeitungsgebühr (2 %): |
+ |
88,00 EUR |
Zinsaufwendungen gesamt
(0,5 % x 32 Monate): |
+ |
704,00 EUR |
| Gesamtschuld: |
= |
5.192,00 EUR |
|
Die Gesamtschuld beläuft sich auf 5.192,00 EUR.
Verteilt auf die gewünschte Laufzeit ergibt sich folgender Tilgungsplan:
31 x 162,00 EUR und 1 x 170,00 EUR.
b) (0,5 % x 32 Monate) x 24 / 32 + 1 = 11,64 %
c) [ (0,5 % x 32 Monate) + 2% ] x 24 / 32 + 1 = 13,09 %
Aufgabe 4:
a)
| Kreditbetrag: |
= |
7.200,00 EUR |
| Bearbeitungsgebühr (2 %): |
+ |
144,00 EUR |
Zinsaufwendungen gesamt
(0,32 % x 30 Monate): |
+ |
691,20 EUR |
| Gesamtschuld: |
= |
8.035,20 EUR |
|
Die Gesamtschuld beläuft sich auf 8.035,20 EUR.
Verteilt auf die gewünschte Laufzeit ergibt sich folgender Tilgungsplan:
29 x 270,00 EUR und 1 x 205,20 EUR.
b) (0,32 % x 30 Monate) x 24 / 30 + 1 = 7,43 %
c) [ (0,32 % x 30 Monate) + 2% ] x 24 / 30 + 1 = 8,98 %
Aufgabe 5:
| Gesamtschuld: |
= |
4.240,80 EUR |
| Kreditbetrag: |
- |
3.800,00 EUR |
| Zinsen und Bearbeitungsgeb.: |
= |
440,80 EUR |
| Bearbeitungsgebühr: |
- |
76,00 EUR |
| Zinsen Ratenkredit: |
= |
364,80 EUR |
|
p = 364,80 x 100 / 3.800,00 = 9,6 % (Zinssatz für 30 Monate)
Zinssatz pro Monat = 9,6 % / 30 Monate = 0,32 % p.m.